Fuzzy c-means clustering C# implementation

воскресенье, 29 марта 2009, Александр Краковецкий

Fuzzy c-means clustering algorithm

The input to the algorithm are the N pixels on the image and the m fuzziness value. Its steps are:

Step 1. Initialize μ with random values between zero and one; but with the sum of all fuzzy membership table elements for a particular pixel being equal to 1 -- in other words, the sum of the memberships of a pixel for all clusters must be one.

Step 2. Calculate an initial value for J using

Equation 1

Step 3. Calculate the centroids of the clusters cj using

Equation 3

Step 4. Calculate the fuzzy membership table using

Equation 2

Step 5. Recalculate J.

Step 6. Go to step 3 until a stopping condition was reached.

Some possible stopping conditions are:

A number of iterations was executed, and we can consider that the algorithm achieved a "good enough" clustering of the data.
The difference between the values of J in consecutive iterations is small (smaller than a user-specified parameter ε), therefore the algorithm has converged.

At the end of the execution of the algorithm we have, for each pixel, the membership values for that pixel in each cluster. Traditionally the algorithm can then defuzzify its results by choosing a "winning" cluster, i.e. the one which is closer to the pixel in the feature space, is the one for which the membership value is highest; and using that cluster center as the new values for the pixel.

Source code explanation

First we need to declare ClusterPoint и ClusterCentroid class for storing point coords.

ClusterPoint.cs

public class ClusterPoint { ///


    /// Gets or sets X-coord of the point
    ///


    public double X { get; set; }

    /// 
    /// Gets or sets Y-coord of the point
    /// 

    public double Y { get; set; }

    /// 
    /// Gets or sets some additional data for point
    /// 

    public object Tag { get; set; }

    /// 
    /// Gets or sets cluster index
    /// 

    public double ClusterIndex { get; set; }

    /// 
    /// Basic constructor
    /// 

    /// X-coord
    /// Y-coord
    public ClusterPoint(double x, double y)
    {
      this.X = x;
      this.Y = y;
      this.ClusterIndex = -1;
    }

    /// 
    /// Basic constructor
    /// 

    /// X-coord
    /// Y-coord
    public ClusterPoint(double x, double y, object tag)
    {
      this.X = x;
      this.Y = y;
      this.Tag = tag;
      this.ClusterIndex = -1;
    }
  }

* This source code was highlighted with Source Code Highlighter.

ClusterCentroid.cs

public class ClusterCentroid : ClusterPoint { ///


    /// Basic constructor
    ///


    /// Centroid x-coord
    /// Centroid y-coord
    public ClusterCentroid(double x, double y)
      : base(x, y)
    {
    }
  }

* This source code was highlighted with Source Code Highlighter.

CMeansAlgorithm.cs

public sealed class CMeansAlgorithm { ///


    /// Array containing all points used by the algorithm
    ///


    private List Points;

    /// 
    /// Array containing all clusters handled by the algorithm
    /// 

    private List Clusters;

    /// 
    /// Gets or sets membership matrix
    /// 

    public double[,] U;

    /// 
    /// Gets or sets the current fuzzyness factor
    /// 

    private double Fuzzyness;

    /// 
    /// Algorithm precision
    /// 

    private double Eps = Math.Pow(10, -5);

    /// 
    /// Gets or sets objective function
    /// 

    private double J { get; set; }

    /// 
    /// Gets or sets log message
    /// 

    public string Log { get; set; }

    /// 
    /// Initialize the algorithm with points and initial clusters
    /// 

    /// Points
    /// Clusters
    /// The fuzzyness factor to be used
    public CMeansAlgorithm(List points, List clusters, float fuzzy)
    {
      if (points == null)
      {
        throw new ArgumentNullException("points");
      }

      if (clusters == null)
      {
        throw new ArgumentNullException("clusters");
      }

      this.Points = points;
      this.Clusters = clusters;

      U = new double[this.Points.Count, this.Clusters.Count];
      //Uk = new double[this.Points.Count, this.Clusters.Count];

      this.Fuzzyness = fuzzy;

      double diff;

      // Iterate through all points to create initial U matrix
      for (int i = 0; i < this.Points.Count; i++)
      {
        ClusterPoint p = this.Points[i];
        double sum = 0.0;

        for (int j = 0; j < this.Clusters.Count; j++)
        {
          ClusterCentroid c = this.Clusters[j];
          diff = Math.Sqrt(Math.Pow(p.X - c.X, 2.0) + Math.Pow(p.Y - c.Y, 2.0));
          U[i, j] = (diff == 0) ? Eps : diff;
          sum += U[i, j];
        }

        double sum2 = 0.0;
        for (int j = 0; j < this.Clusters.Count; j++)
        {
          U[i, j] = 1.0 / Math.Pow(U[i, j] / sum, 2.0 / (Fuzzyness - 1.0));
          sum2 += U[i, j];
        }

        for (int j = 0; j < this.Clusters.Count; j++)
        {
          U[i, j] = U[i, j] / sum2;
        }
      }

      this.RecalculateClusterIndexes();
    }

    /// 
    /// Private constructor
    /// 

    private CMeansAlgorithm()
    {
    }

    /// 
    /// Recalculates cluster indexes
    /// 

    private void RecalculateClusterIndexes() 
    {
      for (int i = 0; i < this.Points.Count; i++)
      {
        double max = -1.0;
        var p = this.Points[i];

        for (int j = 0; j < this.Clusters.Count; j++)
        {
          if (max < U[i, j])
          {
            max = U[i, j];
            p.ClusterIndex = (max == 0.5) ? 0.5 : j;
          }
        }
      }
    }

    /// 
    /// Perform one step of the algorithm
    /// 

    public void Step()
    {
      for (int c = 0; c < Clusters.Count; c++)
      {
        for (int h = 0; h < Points.Count; h++)
        {
          double top = CalculateEulerDistance(Points[h], Clusters[c]);
          if (top < 1.0) top = Eps;

          // Bottom is the sum of distances from this data point to all clusters.
          double sumTerms = 0.0;
          for (int ck = 0; ck < Clusters.Count; ck++)
          {
            double thisDistance = CalculateEulerDistance(Points[h], Clusters[ck]);
            if (thisDistance < 1.0) thisDistance = Eps;
            sumTerms += Math.Pow(top / thisDistance, 2.0 / (this.Fuzzyness - 1.0));
          }
          
          // Then the MF can be calculated as...
          U[h, c] = (double)(1.0 / sumTerms);          
        }
      }

      this.RecalculateClusterIndexes();
    }

    /// 
    /// Calculates Euler's distance between point and centroid
    /// 

    /// Point
    /// Centroid
    /// Calculated distance
    private double CalculateEulerDistance(ClusterPoint p, ClusterCentroid c) 
    {
      return Math.Sqrt(Math.Pow(p.X - c.X, 2) + Math.Pow(p.Y - c.Y, 2));
    }

    /// 
    /// Calculate the objective function
    /// 

    /// The objective function as double value
    private double CalculateObjectiveFunction()
    {
      double Jk = 0;

      for (int i = 0; i < this.Points.Count;i++)
      {
        for (int j = 0; j < this.Clusters.Count; j++)
        {
          Jk += Math.Pow(U[i, j], this.Fuzzyness) * Math.Pow(this.CalculateEulerDistance(Points[i], Clusters[j]), 2);
        }
      }
      return Jk;
    }

    /// 
    /// Calculates the centroids of the clusters 
    /// 

    private void CalculateClusterCenters()
    {
      for (int j = 0; j < this.Clusters.Count; j++)
      {
        ClusterCentroid c = this.Clusters[j];
        double uX = 0.0;
        double uY = 0.0;
        double l = 0.0;

        for (int i = 0; i < this.Points.Count; i++)
        {
          ClusterPoint p = this.Points[i];

          double uu = Math.Pow(U[i, j], this.Fuzzyness);
          uX += uu * c.X;
          uY += uu * c.Y;
          l += uu;
        }

        c.X = ((int)(uX / l));
        c.Y = ((int)(uY / l));

        this.Log += string.Format("Cluster Centroid: ({0}; {1})" + System.Environment.NewLine, c.X, c.Y);
      }
    }

    /// 
    /// Perform a complete run of the algorithm until the desired accuracy is achieved.
    /// For demonstration issues, the maximum Iteration counter is set to 20.
    /// 

    /// Algorithm accuracy
    /// The number of steps the algorithm needed to complete
    public int Run(double accuracy)
    {
      int i = 0;
      int maxIterations = 20;
      do
      {
        i++;
        this.J = this.CalculateObjectiveFunction();
        this.CalculateClusterCenters();
        this.Step();
        double Jnew = this.CalculateObjectiveFunction();
        if (Math.Abs(this.J - Jnew) < accuracy) break; 
      }
      while (maxIterations > i);
      return i;
    }
  }

* This source code was highlighted with Source Code Highlighter.

Test application for Buterfly data clustering

The buterfly data set is shown on the Figure 1.

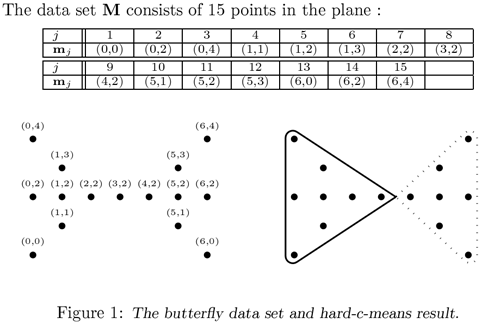
Function to test clustering algorithm:

static void Main(string[] args) { List points = new List(); points.Add(new ClusterPoint(0, 4)); points.Add(new ClusterPoint(0, 2)); points.Add(new ClusterPoint(0, 0)); points.Add(new ClusterPoint(1, 3)); points.Add(new ClusterPoint(1, 2)); points.Add(new ClusterPoint(1, 1)); points.Add(new ClusterPoint(2, 2)); points.Add(new ClusterPoint(3, 2)); points.Add(new ClusterPoint(4, 2)); points.Add(new ClusterPoint(5, 3)); points.Add(new ClusterPoint(5, 2)); points.Add(new ClusterPoint(5, 1)); points.Add(new ClusterPoint(6, 4)); points.Add(new ClusterPoint(6, 2)); points.Add(new ClusterPoint(6, 0)); List centroids = new List(); centroids.Add(new ClusterCentroid(0, 2)); centroids.Add(new ClusterCentroid(6, 2)); CMeansAlgorithm alg = new CMeansAlgorithm(points, centroids, 2); int iterations = alg.Run(Math.Pow(10, -5)); double[,] Matrix = alg.U; for (int j = 0; j < points.Count; j++) { for (int i = 0; i < centroids.Count; i++) { ClusterPoint p = points[j]; Console.WriteLine("{0:00} Point: ({1};{2}) ClusterIndex: {3} Value: {4:0.000}", j + 1, p.X, p.Y, p.ClusterIndex, Matrix[j, i]); } } Console.WriteLine(); Console.WriteLine("Iteration count: {0}", iterations); Console.WriteLine(); Console.WriteLine("Please press any key to exit..."); Console.ReadLine(); } * This source code was highlighted with Source Code Highlighter.