суббота, 25 июня 2011, Александр Краковецкий

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений - как точных, так и численных (приближенных).

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

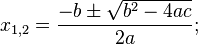
где выражение D = b² − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

• Если D>0, то корней уравнения будет два и оба они будут действительными числами;
• Если D=0, то будет лишь один дейсвительный корень уравнения;
• Если D<0, то действительных решений уравнения нет, а корни будут комплексными.

Для нахождения действительных корней напишем метод SolveQuadraticEquation, входными параметрами которого будут значения при коэффициентах a, b и c, а на выходе – набор значений – решений уравнения:

public Tuple<double,double> SolveQuadraticEquation(double a, double b, double c)
{
  double discRoot = Math.Sqrt(b*b-4.0*a*c);
  double x1 = (-b + discRoot) / (2 * a);
  double x2 = (-b - discRoot) / (2 * a);
  return Tuple.Create(x1, x2);
}

Для работы с комплексными числами в .NET 4.0 был добавлен класс Complex, с помощью которого мы перепишем наш метод для нахождения также и комплексных корней уравнения:

public Tuple<Complex, Complex> SolveQuadraticEquationComplex(double a, double b, double c)
{
  double det = b * b - 4 * a * c;
  double absRoot = Math.Sqrt(Math.Abs(det));
  Complex root = det < 0 ? new Complex(0, absRoot) : new Complex(absRoot, 0);
  Complex q = -0.5 * (b + Math.Sign(b) * root);
  return Tuple.Create(q / a, c / q);
}

Нужно заметить, что в данном случае возвращаться будет набор значений типа Complex.

Для тестирования написанных функций возьмем следующие три квадратных уравнения:

• 5x²+10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
• x²-8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
• x²-5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

namespace ConsoleApp
{
    using System;
    using System.Collections.Generic;
    using System.IO;
    using System.Linq;
    using System.Numerics;
    using NumericalMethods.Equations;

    class Program
    {
        static void Main(string[] args)
        {
            // Redirect output to a file named Files.txt and write file list.
            StreamWriter writer = new StreamWriter(@"out.txt");
            writer.AutoFlush = true;
            Console.SetOut(writer);

            Console.WriteLine("5x^2 - 10x + 200 = 0");
            var results = EquationSolver.SolveQuadraticEquationComplex(5, 10, 200);
            Print(results);

            Console.WriteLine("x^2 - 8x + 16 = 0");
            results = EquationSolver.SolveQuadraticEquationComplex(1, -8, 16);
            Print(results);

            Console.WriteLine("x^2 - 5x + 6 = 0");
            results = EquationSolver.SolveQuadraticEquationComplex(1, -5, 6);
            Print(results);
        }

        private static void Print(IEnumerable<Complex> results)
        {
            for (int i = 0; i < results.Count(); i++)
            {
                Console.WriteLine("x{0} = {1}", i, results.ToList()[i]);
            }
            Console.WriteLine();
        }
    }
}

На выходе получим:

Out.txt:

5x^2 - 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 - 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 - 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Первое уравнение, второе уравнение, третье уравнение.

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

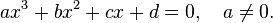
Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

• x^3 - 6x^2 + 11x - 6 = 0
• x^3 - 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

public static IEnumerable<Complex> SolveCubicEquation(double a, double b, double c)
        {
            var Q = (Math.Pow(a, 2) - 3 * b) / 9;
            var R = (2 * Math.Pow(a, 3) - 9 * a * b + 27 * c) / 54;

            if (Math.Pow(R, 2) < Math.Pow(Q, 3))
            {
                var t = Math.Acos(R / Math.Sqrt(Math.Pow(Q, 3))) / 3;
                var x1 = -2 * Math.Sqrt(Q) * Math.Cos(t) - a / 3;
                var x2 = -2 * Math.Sqrt(Q) * Math.Cos(t + (2 * Math.PI / 3)) - a / 3;
                var x3 = -2 * Math.Sqrt(Q) * Math.Cos(t - (2 * Math.PI / 3)) - a / 3;
                return new List<Complex> 
                { 
                    new Complex(x1, 0), new Complex(x2, 0), new Complex(x3, 0)
                };
            }
            else
            {
                var A = -Math.Sign(R) * Math.Pow(Pol(R) + Math.Sqrt(Math.Pow(R, 2) - Math.Pow(Q, 3)), (1.0 / 3.0));
                var B = (A == 0) ? 0.0 : Q / A;

                var x1 = (A + B) - a / 3;

                if (A == B)
                {
                    var x2 = -A - a / 3;
                    return new List<Complex>  { new Complex(x1, 0), new Complex(x2, 0), new Complex(double.NaN, double.NaN) };
                }
                else
                {
                    Complex x2 = new Complex(-(A + B) / 2 - a / 3, -Math.Sqrt(3) * (A - B) / 2);
                    Complex x3 = new Complex(-(A + B) / 2 - a / 3, Math.Sqrt(3) * (A - B) / 2);
                    return new List<Complex>  { new Complex(x1, 0), x2, x3};
                }
            }
        }

Напишем программу для тестирования метода:

namespace ConsoleApp
{
    using System;
    using System.Collections.Generic;
    using System.IO;
    using System.Linq;
    using System.Numerics;
    using NumericalMethods.Equations;

    class Program
    {
        static void Main(string[] args)
        {
            // Redirect output to a file named Files.txt and write file list.
            StreamWriter writer = new StreamWriter(@"out.txt");
            writer.AutoFlush = true;
            Console.SetOut(writer);

            Console.WriteLine("x^3 - 6x^2 + 11x - 6 = 0");
            var results = EquationSolver.SolveCubicEquation(1, -6, 11, -6);
            Print(results);

            Console.WriteLine("x^3 - 6x^2 + 11x + 6 = 0");
            results = EquationSolver.SolveCubicEquation(1, -6, 11, 6);
            Print(results);
        }

        private static void Print(IEnumerable<Complex> results)
        {
            for (int i = 0; i < results.Count(); i++)
            {
                Console.WriteLine("x{0} = {1}", i, results.ToList()[i]);
            }
            Console.WriteLine();
        }
    }
}

Результат выполнения:

Out.txt:

x^3 - 6x^2 + 11x - 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 - 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Первое уравнение, втором случае, второе уравнение.

Решение биквадратных уравнений

Биквадратное уравнение - уравнение четвёртой степени вида

ax⁴ + bx² + c = 0

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x² сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

• 5x^4 - 10x^2 + 200 = 0
• x^4 - 8x^2 + 16 = 0
• x^4 - 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

public static IEnumerable<Complex> SolveBiQuadraticEquation(double a, double b, double c)
        {
            var sol = SolveQuadraticEquationComplex(a, b, c).ToList();
            return new List<Complex> { 
                Complex.Sqrt(sol[0]), 
                -Complex.Sqrt(sol[0]),
                Complex.Sqrt(sol[1]), 
                -Complex.Sqrt(sol[1])};
        }

Напшем программу для тестирования метода:

namespace ConsoleApp
{
    using System;
    using System.Collections.Generic;
    using System.IO;
    using System.Linq;
    using System.Numerics;
    using NumericalMethods.Equations;

    class Program
    {
        static void Main(string[] args)
        {
            // Redirect output to a file named Files.txt and write file list.
            StreamWriter writer = new StreamWriter(@"out.txt");
            writer.AutoFlush = true;
            Console.SetOut(writer);

            Console.WriteLine("5x^4 - 10x^2 + 200 = 0");
            var results = EquationSolver.SolveBiQuadraticEquation(5, 10, 200);
            Print(results);

            Console.WriteLine("x^4 - 8x^2 + 16 = 0");
            results = EquationSolver.SolveBiQuadraticEquation(1, -8, 16);
            Print(results);

            Console.WriteLine("x^4 - 5x^2 + 6 = 0");
            results = EquationSolver.SolveBiQuadraticEquation(1, -5, 6);
            Print(results);
        }

        private static void Print(IEnumerable<Complex> results)
        {
            for (int i = 0; i < results.Count(); i++)
            {
                Console.WriteLine("x{0} = {1}", i, results.ToList()[i]);
            }
            Console.WriteLine();
        }
    }
}

На выходе получим такие результаты:

Out.txt

5x^4 - 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 - 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 - 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.

---