воскресенье, 26 июня 2011, Александр Краковецкий

В прошлой статье мы говорили о решении специальных типов уравнений с помощью точных методов. Сегодня же поговорим о приближенных (численных) методах решения уравнений вида f(x)=0.

В листингах программ есть записи вида:

Helpers.Function(expression, x)

которые соответствуют процедуре получения значения функции, записанной в виде математического выражения в точке x. Фактически, функция Function реализует парсер функций.

Метод половинного деления

Другие названия: метод бисекции (bisection method), метод дихотомии.

Метод половинного деления – простейший численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [x_L; x_R], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:

f(x_L) * f(x_R) < 0.

С непрерывности функции f(x) следует, что на интервале [x_L; x_R] существует, по крайней мере, один корень уравнения (если их несколько, то метод находит один из них).

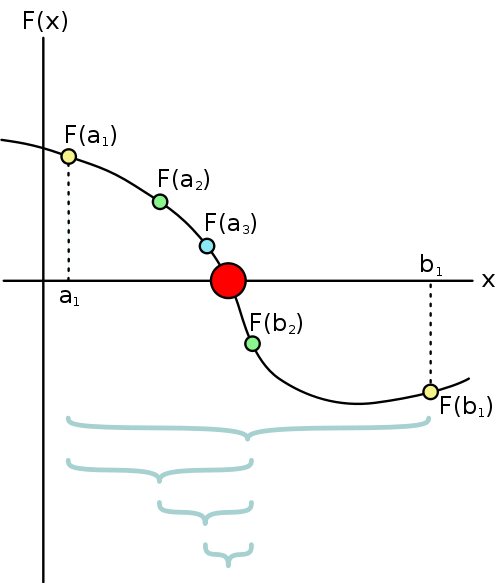
Выберем точку – середину интервала:

x_M = (x_R + x_L) / 2.

Если f(x_M) = 0, то корень найден. Если f(x)≠0, то разобьем этот интервал на два: [x_L; x_M] и [x_M; x_R].

Теперь найдем новый интервал, на котором функция изменяет знак. Повторим описанную процедуру до тех пор, пока не получим требуемую точность или превысим максимально допустимое количество итераций.

Геометрическая интерпретация метода:

Реализация метода на C#:

public static double Bisection(string expression, double Left, double Right, double epsilon = 0.000001)
{
    if (Helpers.Function(expression, Left) * Helpers.Function(expression, Right) >= 0) 
    {
        throw new ArgumentException("F(a) and f(b) should have opposite signs.");
    }

    int iterationCount = 0;
    double c;

    do
    {
        c = (Left + Right) / 2;

        if (Helpers.Function(expression, Left) * Helpers.Function(expression, c) < 0)
        {
            Right = c;
        }
        else
        {
            Left = c;
        }

        if (Math.Abs(Helpers.Function(expression, c)) <= epsilon || (Right - Left) <= epsilon || iterationCount == 1000)
        {
            break;
        }

        iterationCount++;
    }
    while (true);

    return c;
}

Метод секущих

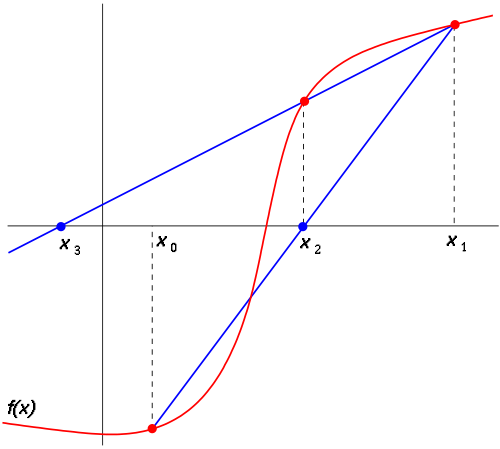
Другие названия: метод хорд (secant method);

Метод хорд – еще один численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [x₀; x₁], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:

f(x_L) * f(x_R) < 0.

Последующие приближения находят по формуле:

x_n+1) = x_n-(f(x_n )/(f(x_n)-f(x_n-1)) * (x_n - x_n-1), n=1, 2, …

Геометрическая интерпретация метода:

Реализация метода на C#:

public static double Secant(string expression, double xa, double xb, double epsilon = 0.00001)
{
    double xlast;
    double x = 0;
    if (Helpers.Function(expression, xa) * Helpers.Function(expression, xb) >= 0)
    {
        throw new ArgumentException("F(a) and f(b) should have opposite signs.");
    }

    var iter = 0;
    do
    {
        xlast = x;
        x = xb - Helpers.Function(expression, xb) * (xb - xa) / (Helpers.Function(expression, xb) - Helpers.Function(expression, xa));

        if (Helpers.Function(expression, x) * Helpers.Function(expression, xa) > 0)
        {
            xa = x;
        }
        else
        {
            xb = x;
        }

        iter++;
    }
    while (Math.Abs(x - xlast) > epsilon || (xb - xa) <= epsilon || iter == 1000);

    return x;
}

Метод простых итераций

Уравнение f(x)=0 с помощью некоторых преобразований необходимо переписать в виде x=φ(x).

Уравнение f(x)=0 эквивалентно уравнению x=x+λ(x)f(x) для любой функции λ(x)≠0. Возьмем φ(x)=x-λ(x)f(x) и выберем функцию (или переменную) λ(x)≠0 так, чтобы функция φ(x) удовлетворяла необходимым условиям.

Для нахождения корня уравнения x=φ(x) выберем некоторое начальное значение x₀, которое должно находиться как можно ближе к корню уравнения. Дальше с помощью итерационной формулы x_n+1=φ(x_n) будем находить каждое следующее приближение корня уравнения.

Пример: x²-5x+6=0

Преобразования в вид x=φ(x):

x²-5x=-6, x*(x-5)=-6, x=-6/(x-5)=φ(x).

Реализация метода на C#:

public static double SimpleIterations(string expression, double xa, double epsilon = 0.00001)
{
    double x = 0.0;
    double xPrev = xa;

    var iter = 0;
    do
    {
        x = Helpers.Function(expression, xPrev);

        if (Math.Abs(x - xPrev) <= epsilon || iter == 1000){
            break;
        }

        xPrev = x;
        iter++;
    }
    while (true);

    return x;
}

Метод Вегштейна

Метод Вегштейна является модификацией метода секущих, однако его можно назвать и улучшенным методом простой итерации, преобразовав вычислительную формулу к виду:

Это двухшаговый метод, и для начала вычислений необходимо задать 2 приближения x_a и x_b.

Реализация метода на C#:

public static double Wegstein(string expression, double xa, double xb, double epsilon = 0.00001) { double x = 0.0;

    var iter = 0;
    do
    {
        x = xb - (xb - Helpers.Function(expression, xb)) / (1 - (Helpers.Function(expression, xb) - Helpers.Function(expression, xa)) / (xb - xa));

        if (Math.Abs(x - xb) <= epsilon || iter == 1000)
        {
            break;
        }

        xa = xb;
        xb = x;
        iter++;
    }
    while (true);

    return x;
}

Метод Ньютона

Если - начальное приближение корня уравнения f(x) = 0, то последовательные приближения находят по формуле:

Если f' и f'' непрерывны и сохраняют определенные знаки на отрезке , а f(a)f(b) < 0 , то, исходя из начального приближения удовлетворяющего условию можно вычислить с любой точностью единственный корень уравнения f(x) = 0.

Геометрическая интерпретация метода:

Реализация метода на C#:

public static double Newton(string expression, string derivativeExpression, double x, double epsilon = 0.00001)
{
    int t = 0;
    double x1, y;
    do
    {
        t++;
        x1 = x - Helpers.Function(expression, x) / Helpers.Function(derivativeExpression, x);
        x = x1;
        y = Helpers.Function(expression, x);
    }
    while (Math.Abs(y) >= epsilon);
    return x;
} 

---